An experiment on the Accuracy Improvement of
Photogrammetrically derived DEM
Carlos López
Centro de Cálculo, INCO
Facultad de Ingeniería CP 11300
Julio Herrera y Reissig 565, Montevideo, URUGUAY
Ph. +5982 7114229; Fax +5982 7115446
Email: carlos.lopez@ieee.org
Keywords: DEM, accuracy assessment of source data, grid data, quality controlAbstract
This paper focus on a topic barely considered in the literature: how to improve the accuracy of a given DEM, pointing out to its most suspicious values. Hannah, 1981; Felicísimo, 1994 and López, 1997, 2000 suggested methods to do so. Their work do not assume any production process (photogrammetric, direct measurement, etc.) or source (contour maps, remote sensing image, etc.); they provide algorithms to check the given DEM as is pointing out to its most unlikely values. However, only López, 2000 compare the methods with a real example taken from a hilly area. The usefulness for blind application to other landscapes remained unclear. This paper summarizes the results of a comparison of those methods using six DEM´s intended to be representative of different landscapes. Two outlier detection methods have been applied to each DEM, producing each a prescribed number of height candidates to be analyzed, and those values have been blindly replaced by interpolated heights. The so improved (or degraded) DEM is compared against the ground truth, and updated accuracy figures are calculated. The accuracy as RMSE obtained by the method by López, 2000 (L2000) typically outperforms the one of Felicísimo, 1994 (F1994) in all except one of the cases irrespective of the landscape. By changing selected (up to 1 per cent of the) heights of the dataset the RMSE diminishes an amount between 2 and 8 per cent of the original value.
1. Introduction
DEM are one of the most popular datasets in GIS applications. They are used in visibility analysis, landslide evaluation, erosion, etc. being all different requirements with also different needs of accuracy. Recent efforts in the GIS community focused in the analysis of the propagation of errors for a given operation (Defourny et al.,1998; Fortin et al. 1998), or the establishment of the knowledge about how to cope with the inherent uncertainty of the dataset (Fortin et al. 1998). This will raise concerns among users about the effect of outliers on the final results, and motivate efforts to use reliable and effective "cleaning" tools (if available!).Some of the references regarding error propagation assume that the DEM is contaminated with just errors following a normal distribution, which might not be the case in many particular DEM. Most of the literature on accuracy improvement have been designed from the producer side, assuming that the system "...warns the operator about suspicious values..." and some correction measure can be taken. End users are left alone, because they do not have access to the original sources (aerial photographs, control points, etc.). Error surfaces stating the expected range of variation for a given confidence level (which are commonplace in the geostatistics community) are barely presented together with the DEM. Thus, if the application is sensitive to the accuracy of the DEM, there is little help for the end user, because a) no tool to pinpoint for unlikely values are available and b) once selected and confirmed that some elevation points are unrealistic, there is no help to interpolate reliable values from the others.
Regarding the first aspect, there are few references in the literature. A deterministic approach was used in an early paper by Hannah, 1981, who detects non-systematic errors by applying constraints to the slopes and to the changes in slope at each point. Felicísimo, 1994 analyzed the differences between the elevation and an interpolated value from the neighbors. Assuming gaussian distribution of the errors, he analyzed the differences by means of a standard Student t test. No experimental result is given. López, 1999 described a method based in the decomposition of the regular grid DEM into strips, and consider it as a multivariate table. Standard statistical techniques have been applied to select the unlikely elevations. He illustrated the performance of the method using synthetic errors only. López, 2000 extended his previous method and showed results using a real DEM with real errors from a mountain. Its ability for other landscapes remains unknown. All of the abovementioned methods are valid disregarding the lineage of the DEM, i.e. irrespective if it has been generated by direct photogrammetric measurements, digitizing contour lines, field survey, etc. Thus, they do not consider systematic errors, because they are mostly connected with the generation procedure.
The second issue has been extensively considered in the literature for DEM generation, and will not be analyzed here. This paper will compare two of the available methods for detecting outliers in six different landscapes; in some sense, it can be complementary to the work of López, 2000. In a companion paper (Durañona et al., 2000) a computer implementation of all the codes is described.
2. Data
We will use the set of DEMs for six test areas (see table 1) produced by the international working group III of the ISPRS in 1983, described by Torlegård et al., 1986 and Tolstoy et al., 2000. They were chosen to represent a variety of terrain types regarding land use, vegetation and surface roughness. For each of them, a number of low accuracy and one with higher accuracy DEMs have been derived. We will use one of the former as input, and make comparisons using the later as a reference.
|
|
|
|
(%) |
|
|
|
|
Spitze (Germany) |
|
|
|
Smooth terrain |
|
|
Sohnstetten (Germany) |
|
|
|
Hills of moderate height |
|
|
Stockholm (Sweden) |
|
|
|
Urban communication areas |
|
|
Bohuslan (Sweden) |
|
|
|
Rugged granite bedrock without soil cover |
|
|
Uppland (Sweden) |
|
|
|
Farmland and forest |
|
|
Drivdalen (Norway) |
|
|
|
Steep and rugged mountains |
Table 1 Summary of the characteristics of the available DEMs (from Torlegård et al., 1986)
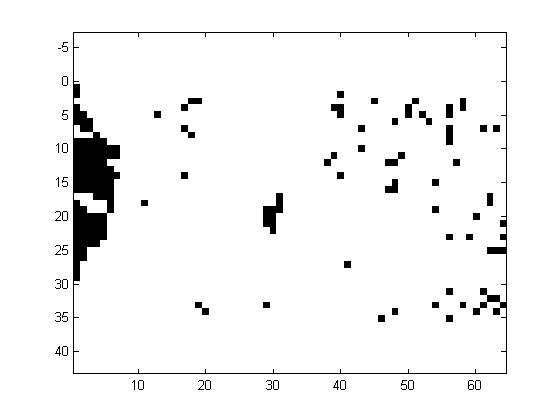
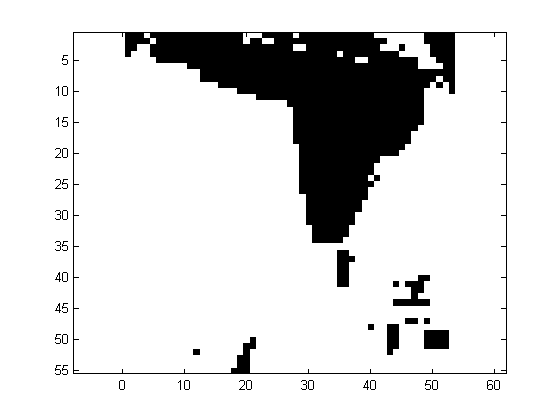
Despite the elevation data is located in a regular grid, there is no data in forest areas. The coverage (in percent) is also indicated in table 1. The following description has been taken in part from Östman, 1987. "...The Spitze test area is located in the northern part of Germany. The landscape is very smooth, except for a dense forest in the western part of the area. The Sohnstetten test area is located in Germany. The landscape consists of undulated hills of moderate height. The Stockholm area is an example of mixed urban and natural forest. It is crossed by highways and has a park in its central part. The Bohuslan test area is located on the West Coast of Sweden. The landscape consists mainly of solid rock and the vegetation coverage is very sparse. There are also some quarries in the area and the terrain surface is fairly rough. The Uppland test area is located in the central part of Sweden, just north of Stockholm. The landscape is fairly smooth with tree covered hills scattered over the farmland. The tree coverage is sparse and no part of the test area had to be excluded due to dense tree coverage. The Drivdalen test area is located in Norway, and is an example of steep and rugged terrain..."The pattern of missing elevations is irregular, being rather isolated spots or contiguous areas, as illustrated in Fig. 1. In order to apply the methods, the datasets have been imputated using bilinear interpolation.


Figure 1 Example of an isolated (Spitze, left) and contiguous (Bohusland, right) pattern of missing elevations, denoted in black.
3. Results
Due to space constraints, only some figures could be summarized in Table 2. For example, the entry 4.393 for Sohnstetten in the second column indicates that, after selecting just 1 per cent of the elevations of the DEM and blindly imputating them, the method F1994 diminishes the RMSE in 4.393 per cent. The imputation procedure uses bilinear approximation based upon the 8 surrounding elevations. If the imputation were perfect, after selecting 100 per cent of the elevations the RMSE should decrease 100 per cent also. The 1 per cent effort was chosen following Torlegård et al., 1986, and is of the order of the number of outliers found in the DEM's. Since the RMSE is badly affected by even few outliers, we have also considered the percentile 95 per cent of the absolute errors as a significant figure.
|
|
acc(0%) |
p95(0%) |
|
|
|
||
|
|
|
|
|
|
|
||
| Spitze |
|
|
|
|
|
|
|
| Sohnstetten |
|
|
|
|
|
|
|
| Stockholm |
|
|
|
|
|
|
|
| Bohuslan |
|
|
|
|
|
|
|
| Uppland |
|
|
|
|
|
|
|
| Drivdalen |
|
|
|
|
|
|
|
Table 2 Summary of the results of the test."acc(x%)" stands for accuracy (as RMSE) after editing x% of the elevations in the DEM., while "p95(x%)" stands for the percentile 95% of the elevation error. DEM id. identifies which particular DEM was used in the test (see Tolstoy et al., 2000)
Despite encouraging, the results should be analyzed with some caution. Some of the test sites were too small in size, a situation outside the hypothesis of the method L2000, while the F1994 method is less demanding. The method L2000 requires an undefined "large" number of rows and columns, which is not the case in any DEM (for Sohnstetten there are only 20 rows for the analysis!). In addition, the missing elevations have been interpolated, and both methods were applied after the interpolation, which might introduce further disturbances.This explains why the performance is not as good as reported before (López, 2000). However, for all except Bohuslan, the RMSE efficiency of method L2000 exceeded 1.96 per cent, while the F1994 did not. Bohuslan has a particular pattern of missing values, which might have affected adversely the performance of both methods. For all test areas and for method L2000, we performed the operations for various parameter values, and presented the best figures.
For example, for the Spitze test area, the results show a clear advantage for the method L2000 vs. F1994. The achievable accuracy with L2000 for an effort of 1 per cent is 0.148 m, while for the same effort the F1994 is 0.160 m RMSE (7.5 per cent better). The error values are (for the same effort) in the range [-0.592 0.728] vs. [-2.716 1.135]. This performance is optimal for the strip width equal to 5, and 2 terms uncontrolled, which are the parameter values suggested by the criteria described in López, 2000, and defined there. The complete results for this and the other test areas will be presented in full in a paper under preparation.
4. Conclusions
We have presented preliminary quantitative results of the comparison of two methods for outlier detection for DEM, applied over six cases representative of different landscapes. The procedures can be applied by either a DEM producer or an end user. This paper illustrates the type of tools to be required in the near future for the managing of uncertainty and errors in GIS. Once an outlier is detected, we blindly imputated it using bilinear approximation. The results in terms of RMSE or percentile 95 per cent demonstrated that a significant improvement in the accuracy for both methods can be achieved, being the most reliable results for the method by López, 2000 irrespective of the terrain. In some cases, by blindly imputate 1 per cent of the elevations the RMSE can be reduced up to 8.642 per cent. These results should be taken with caution and can be regarded as conservative, because the DEM samples were not particularly appropriate for its application due to its small size.
References
- Defourny, P.; Hecquet, G. and Philippart, T. 1998 Digital Terrain Modeling: Accuracy assessment and hydrological simulation sensitivity. In Spatial Accuracy Assessment: Land Information Uncertainty in Natural Resources, ISBN 1-57504-119-7. Eds. Lowell, K. and Jaton, A. 61-70
- Durañona, G. and López, C. 2000. DM4DEM: A GRASS-compatible tool for blunder detection of DEM. In Proceedings of the 4th. International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences, Amsterdam, The Netherlands, 2000.
- Felicísimo, A., 1994, Parametric statistical method for error detection in digital elevation models. ISPRS J. of Photogrammetry and Remote Sensing, 49, 4, 29-33.
- Fortin, M.; Edwards, G. and Thomson, K. P. B. 1998 The role of error propagation for integrating multisource data within spatial models: the case of the DRASTIC groundwater vulnerability model. In Spatial Accuracy Assessment: Land Information Uncertainty in Natural Resources, ISBN 1-57504-119-7. Eds. Lowell, K. and Jaton, A. 437-443
- Hannah, M. J., 1981, Error detection and correction in Digital Terrain Models. PE&RS 47, 1, 63-69.
- López, C., 1997. Locating some types of random errors in Digital Terrain Models. International Journal of Geographic Information Science, 11, 7, 677-698.
- López, C., 2000. On the improving of elevation accuracy of Digital Elevation Models: a comparison of some error detection procedures Transactions in GIS, 4, 1, 43-64
- Östman, A., 1987, Quality Control of Photogrammetrically sampled Digital Elevation Model using an On-line graphical DEM Editor. Photogrammetric Record, 12, 69, 333-341
- Tolstoy, R.; López, C. and Torlegård, K., 2000, The ISPRS WG III:3 International Comparative Test of Photogrammetrically Sampled Digital Elevation Models 1982: Description of the dataset. Unpublished manuscript
- Torlegård, K; Östman, A. and Lindgren, R., 1986, A comparative test of photogrammetrically sampled digital elevation models. Photogrammetria, 41, 1, 1-16