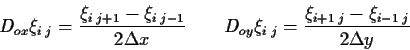Next: Tridiagonal system
Up: Finite differences scheme
Previous: Column-wise j implicit sweep
Finite differences operators
The operators Dox and Doy are defined by (4.10)
to (4.14) (Gustafsson et al., 1995; Hirsch, 1991)7.2.
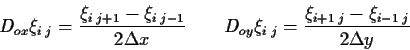 |
(7.7) |
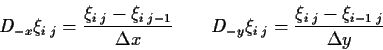 |
(7.8) |
 |
(7.9) |
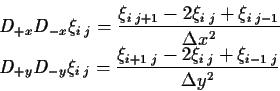 |
(7.10) |
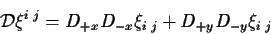 |
(7.11) |
Elias Kaplan M.Sc.
1998-07-22